QUESTION: (ÉTÉ2016) Je calcule les proportions d’une poutre en I monosymétrique dont l’élancement de l’âme, h/w, respecte de façon marginale la limite de classe 3 pour les profilés en W en flexion pure selon le tableau 2 de la norme S16-09. Cette limite s’applique-t-elle aux profilés monosymétriques? apply to mono-symmetric sections?
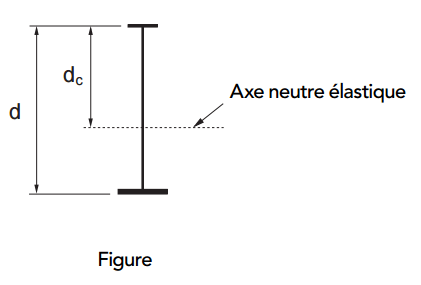
RÉPONSE: Non, les limites pour les profilés en I fournies dans le tableau 2 de la norme S16-09 s’appliquent aux profilés à ailes égales. La norme CSA S6, le Code canadien sur le calcul des ponts routiers, aborde les limites de classe 3 relatives à l’âme des profilés en I monosymétriques à l’article 10.10.3.1. Dans cet article, la valeur de h est remplacée par 2dc, dc représentant la distance de l’axe neutre à la fibre extrême en compression (voir la figure).
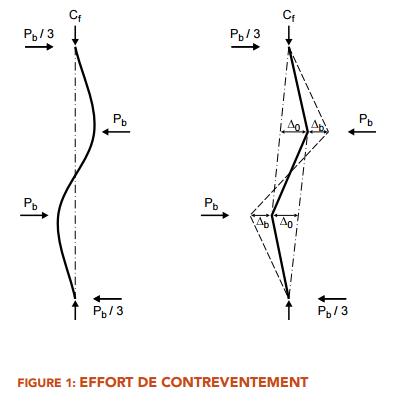
QUESTION: (2015) En utilisant la méthode directe conformément à l’article 9.2.6.2 de la norme CSA S16-F14, j’ai été surpris de constater que, pour un effort dans le poteau (Cf) donné, l’effort de contreventement (Pb) augmente lorsqu’on passe de un à deux contreventements. Est-ce que je comprends bien?sense?
RÉPONSE: Intuitivement, on pourrait croire que d’ajouter des contreventements pour stabiliser une pièce comprimée devrait réduire les forces appliquées sur chaque contreventement puisqu’ils sont plus nombreux à « partager » ces forces. C’est pourtant le contraire qui se produit. Il faut noter que les forces d’appui de deux contreventements adjacents n’agissent pas dans la même direction, mais font plutôt le contraire (Figure 1). Avec un effort dans le poteau (Cf) donné et en respectant la tolérance d’aplomb maximum (∆0/L), l’effort de contreventement (Pb) est directement proportionnel au facteur β, qui prend des valeurs de 2 et 3 pour 1 et 2 contreventements positionnés à intervalles réguliers, respectivement. Dans ce cas, l’effort de contreventement (Pb) augmente de 50 %.
QUESTION: (ÉTÉ2015) Comme cela est indiqué dans le Commentaire sur la norme S16-09, les expressions d’élancement prévues à la Clause 13.3.3 pour les « pièces comprimées à une seule cornière » ne sont pas destinées aux contreventements dans les cadres contreventés. Je veux utiliser des contreventements comprimés à ailes égales dans un cadre contreventé. Comment dimensionne-t-on ces contreventements à une seule cornière?
RÉPONSE: Les contreventements à une seule cornière sont généralement utilisés comme contreventements en traction seulement en raison de leur résistance limitée à la compression. Pour résister à une forte compression avec une seule aile assemblée, ils doivent être dimensionnés comme des poteaux soumis à des charges excentriques. Dans ce cas, la clause 13.3.2 traite des résistances au flambement en flexion et en flexiontorsion et la Clause 13.8.3 traite de la compression et de la flexion axiales combinées.
QUESTION: (2014) Je calcule la résistance à la flexion d’une section à symétrie simple en I non maintenue latéralement et ayant des semelles d’épaisseurs différentes. Quelle doit être la valeur de t dans les expressions de βx et de Cw fournies dans l’alinéa 13.6 (e) de S16-09?
RÉPONSE: Dans les deux expressions, la valeur de « d-t » peut être la distance entre les centres de gravité des semelles. Cw peut également être calculée à l’aide de la formule fournie sous Built-up Sections dans la Partie 6 du Handbook of Steel Construction de l’ICCA.
QUESTION: (ÉTÉ2014) Je suis en train de concevoir une charpente de bâtiment comportant un simple cadre gravitaire et un cadre rigide périmétrique servant de système de résistance aux forces horizontales. Il n’y a pas de baie contreventée ni de mur à effet de cisaillement. Plusieurs poteaux gravitaires sont soumis à un moment de flexion important selon l’axe fort en raison d’une excentricité prononcée de l’assemblage. Ces poteaux à ailes larges devraient-ils être conçus comme les assemblages poutrepoteau d’un cadre non contreventé? Comment calcule-t-on les valeurs pour U1x?
RÉPONSE: Non, il s’agit ici d’un cadre contreventé. Malgré l’absence d’un portique contreventé, les poteaux gravitaires ne sont pas des éléments essentiels du système de résistance aux forces horizontales. On peut calculer les valeurs U1x selon la clause 13.8.4 de la norme CSA S16 mais en veillant à ce que les valeurs U1x pour la résistance transversale et la résistance au déversement ne soient pas inférieures à 1.0.
QUESTION: (PRINTEMPS2014) J’ai entendu parler de l’exigence de charge fictive dans le calcul des charpentes de bâtiment mais je ne parviens pas à trouver la disposition concernant les charges fictives dans le code du bâtiment. Où puis je la trouver?
RÉPONSE: Vous trouverez la disposition sur les charges fictives dans la norme CSA S16-09, Règles de calcul des charpentes en acier. La norme autorise la prise en compte des effets de deuxième ordre liés aux charges de gravité s’exerçant sur la configuration déplacée d’une structure subissant des charges horizontales au moyen d’une analyse des effets P-delta. En outre, les effets liés à la déstabilisation et à la plastification partielle peuvent être calculés de façon approchée par Nous vous invitons à poser vos questions sur divers aspects de la conception et de la construction des bâtiments en acier. L’ICCA reçoit un très grand nombre de questions; nous ne pouvons en publier que quelques-unes dans cette rubrique. L Outstanding leg (An3) (a) (b) Effective Net Area Figure 1 x w2 Connected leg (An2) L Outstanding leg (An3) (a) (b) Effective Net Area Figure 1 x w2 Connected leg (An2) FIGURE 1 – AIRE NETTE EFFICACE un ensemble de charges horizontales, qui sont qualifiées de charges fictives. La charge fictive à appliquer à chaque étage en plus de toute autre charge horizontale est comptée comme étant égale à 0,5 % de la charge de gravité coexistante exercée sur cet étage. Sinon, une rigoureuse analyse de second ordre prenant en compte à la fois la non-linéarité géométrique, y compris la déstabilisation, et la plastification partielle peut aussi être employée.
QUESTION: (AUTOMNE2013) Lors du contrôle du flambement en flexion d’un profilé en C sous une sollicitation axiale, quel rayon de giration doit être utilisé pour calculer Fex et Fey?
RÉPONSE: Selon S16-09, article 13.3.2, les contraintes de flambement élastique sont les suivantes:
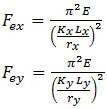
Pour les sections à simple symétrie tels que les profilés en C, le même article précise que l’axe y est considéré comme étant l’axe de symétrie. Dans les tables de propriétés et de dimensions des profilés en C de la partie 6 du Handbook of Steel Construction, c’est l’axe x qui est défini comme étant l’axe de symétrie. Par conséquent, Fex devra être calculé en utilisant le rayon de giration ry fourni dans les tables du Handbook, de même Fey sera calculé en utilisant rx.
QUESTION: (AUTOMNE2012) Comment dois-je calculer la résistance élastique à la flexion d’une plaque en porte-à-faux soumise à un déversement?
RÉPONSE: Pour une plaque encastrée soumise à un moment de flexion selon son axe fort mais sans soutien latéral, le Guide to Stability Design Criteria for Metal Structures, 6th Edition (R.D. Ziemian, John Wiley & Sons, 2010) fournit des expressions pour le moment de flambement élastique (Mu), en fonction de la hauteur de du point d’application de la charge. Par exemple, lorsque la plaque est soumise àune charge ponctuelle à son extrémité:
a) Pour une charge sur la surface supérieure »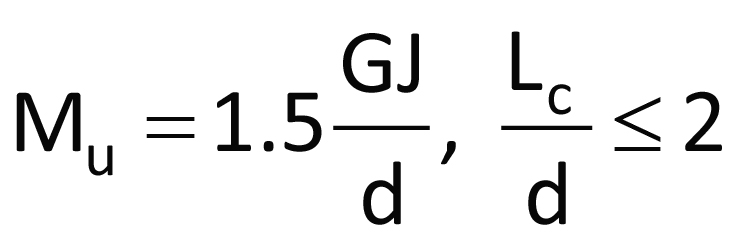 b) Pour une charge au centre de cisaillement:
b) Pour une charge au centre de cisaillement:
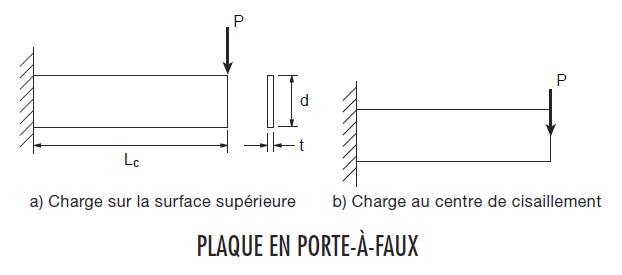 NOTE: Dans le numéro 44 de la revue Avantage Acier, cette rubrique fait référence au moment de déversement élastique de porte-à-faux indiqué dans le Guide to Stability Design Criteria for Metal Structures, 6e édition. Comparativement à des études récentes utilisant l’analyse par éléments finis, l’expression « Mc = 1.5GJ/d » offre des valeurs imprudentes pour les plaques (section rectangulaire) et les longs porte-à-faux de profilé en I qui sont sujets au déversement. Il faut éviter de l’utiliser pour les porte-à-faux en plaques qui sont plus longs que le double de leur profondeur.
NOTE: Dans le numéro 44 de la revue Avantage Acier, cette rubrique fait référence au moment de déversement élastique de porte-à-faux indiqué dans le Guide to Stability Design Criteria for Metal Structures, 6e édition. Comparativement à des études récentes utilisant l’analyse par éléments finis, l’expression « Mc = 1.5GJ/d » offre des valeurs imprudentes pour les plaques (section rectangulaire) et les longs porte-à-faux de profilé en I qui sont sujets au déversement. Il faut éviter de l’utiliser pour les porte-à-faux en plaques qui sont plus longs que le double de leur profondeur.
QUESTION: (ÉTÉ2012) Lors de la conception de poutres continues et de poutres du système Gerber (Figure 1), peut-on déduire les points d’inflexion contreventés latéralement contre le déversement?
RÉPONSE: Il ne faut pas confondre les points d’inflexion dans le diagramme des moments fléchissants verticaux avec les points d’inflexion dans le flambement latéral. En général, on ne connaît pas le flambement latéral au stade de la conception. Les points d’inflexion dans le diagramme des moments fléchissants ne coïncidant pas avec ceux du flambement latéral, ils ne doivent pas être considérés comme étant contreventés latéralement, sauf s’ils sont contreventés.

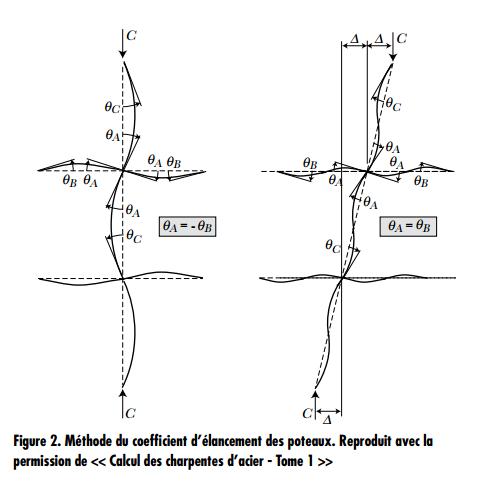
QUESTION: (ÉTÉ2012) J’ai employé la méthode du coefficient d’élancement pour concevoir des poteaux dans des cadres avec oscillation et des cadres sans oscillation. En revanche, je ne trouve pas le nomogramme du coefficient d’élancement pour les cadres avec oscillation dans la norme CSA S16. La méthode du coefficient d’élancement est-elle toujours valide?
ANSWER:
La méthode du coefficient d’élancement des poteaux s’efforce de donner une valeur approximative de la charge critique élastique des poteaux dans un cadre ordinaire qui est dépourvu de moments primaires et qui comporte des poutres identiques à chaque niveau et des poteaux identiques (voir la Figure 2). Ce modèle de cadre idéal ne tient absolument pas compte des effets du second ordre dans les poutres. De plus, par rapport aux méthodes d’analyse modernes qui tiennent compte des effets du second ordre, etc., elle est généralement incapable de donner des résultats précis pour les cadres réels. Depuis l’adoption de la norme S16.1-M89, la méthode du coefficient d’élancement a été abandonnée au profit des cadres avec oscillation. C’est pourquoi le nomogramme pour les cadres avec oscillation a été exclu.
Lorsqu’on utilise une analyse élastique, la norme actuelle S16-09 prévoit l’application d’une analyse de second ordre qui tient directement compte des effets de l’oscillation. Par ailleurs, les effets P-delta sont inclus au moyen du coefficient d’amplification (U2). De plus, on applique les charges théoriques pour tenir compte des effets de la plastification partielle et de l’absence d’aplomb initiale.
Remarque : Lorsque les effets P-delta et les charges théoriques sont pris en compte, l’utilisation du coefficient d’élancement des poteaux pour la conception d’un cadre sans oscillation (K ≤ 1) est acceptable aux fins de considération du déversement. Cette méthode suppose toutefois que tous les éléments de la structure conservent leur élasticité avant de flamber. C’est pourquoi les exigences poteaux solides/poutres faibles pour la construction non conventionnelle, le cas échéant, en font une option inadaptée.
QUESTION: (PRINTEMPS2012) Lorsque j’utilise le coefficient d’intensification U2 pour tenir compte des effets P- Δ conformément à S16, devrais-je aussi appliquer U2 aux charges conceptuelles?
RÉPONSE: Oui, les charges conceptuelles doivent également être intensifiées lorsque U2 est utilisé pour tenir compte des effets P- Δ.
QUESTION: Part A: (AUTOMNE2011) Comment dois-je calculer la résistance à la compression axiale d’un membre sujet au voilement élastique?
ANSWER: Two methods are provided in CSA Standard S16-09, the effective area method and the effective yield stress method.
La norme CSA S16-09 fournit deux méthodes, soit la méthode de l’aire efficace et la méthode de la limite d’élasticité effective.
Méthode de l’aire efficace
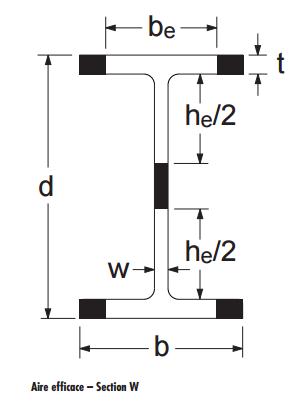
Les ingénieurs sont généralement familiarisés avec le concept d’aire efficace pour le calcul des poteaux soumis au voilement élastique. On s’attend à ce que de telles sections soient sujettes au voilement avant d’atteindre la charge de plastification en compression axiale, AFy. Elles sont calculées selon la Clause 13.3.5 (a) de la norme CSA S16-09 lorsque le rapport de largeur à épaisseur des ailes ou de l’âme dépasse les limites données au Tableau 1 de S16-09. Lors du calcul de la résistance à la compression axiale, une partie de la section est considérée inefficace et est donc omise. Pour une section à larges ailes, par exemple, l’aire efficace de la section, Ae, est calculée comme suit : si les ailes dépassent le rapport maximal de largeur à épaisseur du Tableau 1, l’aire des extrémités (parties ombragées de la figure) est supprimée, de telle façon que la largeur efficace restante de l’aile satisfasse le rapport maximal ; de même, la hauteur efficace de l’âme est prise comme étant he comme on le voit sur la figure. Les parties efficaces des ailes et de l’âme constituent ensemble l’aire efficace, Ae.
Méthode de la limite d’élasticité effective
La méthode de la limite d’élasticité effective est peut-être moins connue. S16-09 autorise également cette méthode pour calculer la résistance à la compression axiale. Selon ce concept, initialement introduit dans S16-01, l’aire de la section reste intacte, mais la limite d’élasticité est réduite pour prendre en compte le voilement. La limite d’élasticité effective, Fye, est prise comme étant la limite d’élasticité réduite déterminée à partir du rapport de largeur à épaisseur respectant la limite du Tableau 1. Si les ailes et l’âme sont toutes les deux sujettes au voilement élastique, deux limites élastiques effectives distinctes sont calculées. Dans un but de simplicité, la résistance du membre est basée sur la plus basse des deux valeurs.
QUESTION: Part B: (AUTOMNE2011) Est-ce que les méthodes fournies dans CSA S16-09 donnent la même réponse?
RÉPONSE: Non, la méthode de l’aire efficace et la méthode de la limite d’élasticité effective ne donnent généralement pas la même réponse. Un exemple est présenté ci-dessous pour illustrer les deux méthodes. Considérons un poteau W360x72 en acier ASTM A992 supporté latéralement (L = 0). L’aire de la section est A = 9100 mm2 et la limite d’élasticité spécifiée, Fy, = 345 MPa. La résistance pondérée à la compression axiale est déterminée sur la base (1) de l’aire efficace et (2) de la limite d’élasticité effective.
(1) Méthode de l’aire efficaceVérifiez les rapports de largeur à épaisseur des ailes et de l’âme:
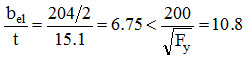 Les ailes ne sont pas sujettes au voilement.
Les ailes ne sont pas sujettes au voilement.
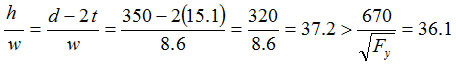 L’âme est sujette au voilement élastique. La hauteur efficace de l’âme est donnée par:
L’âme est sujette au voilement élastique. La hauteur efficace de l’âme est donnée par:
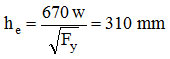 L’aire efficace est:
L’aire efficace est:
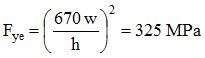 Et la résistance à la compression est:
Et la résistance à la compression est:
Bien que seulement l’âme soit sujette au voilement, la section en entier est affectée par la diminution de la limite d’élasticité. Pour cette raison, la méthode de l’aire efficace se solde en une plus grande résistance (pour un élément supporté latéralement) que la méthode de la limite d’élasticité effective dans cet exemple particulier. Toutefois, la méthode de la limite d’élasticité effective produit habituellement une plus grande résistance pour les membres élancés.
Pour les deux méthodes, la contrainte de flambement élastique, Fe, est déterminée à l’aide des propriétés de la section brute.
QUESTION: Part C: (AUTOMNE2011) Quelle méthode est utilisée pour calculer les valeurs des sections sujettes au voilement élastique dans les tableaux de poteaux et les tableaux de contrefiche à cornière dans le Manuel de l’ICCA?
RÉPONSE: Les deux méthodes sont utilisées pour calculer les résistances pondérées à la compression, Cr, pour les poteaux W sujets au voilement élastique et les valeurs sous forme de tableaux sont les plus grandes des deux. Seule la méthode de l’aire efficace est utilisée pour calculer les valeurs de Cr pour d’autres poteaux et contrefiches. Les sections de cornières qui dépassent la limite de b à t du Tableau 1 sont exclues des tableaux de contrefiche à cornière en forme d’étoile.
