QUESTION: (ÉTÉ2016) Je calcule les proportions d’une poutre en I monosymétrique dont l’élancement de l’âme, h/w, respecte de façon marginale la limite de classe 3 pour les profilés en W en flexion pure selon le tableau 2 de la norme S16-09. Cette limite s’applique-t-elle aux profilés monosymétriques?
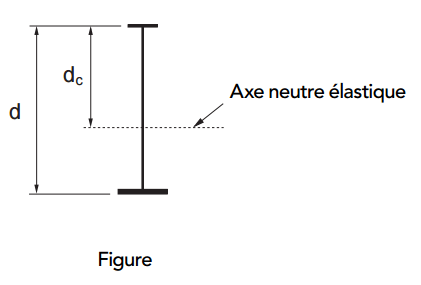
RÉPONSE: Non, les limites pour les profilés en I fournies dans le tableau 2 de la norme S16-09 s’appliquent aux profilés à ailes égales. La norme CSA S6, le Code canadien sur le calcul des ponts routiers, aborde les limites de classe 3 relatives à l’âme des profilés en I monosymétriques à l’article 10.10.3.1. Dans cet article, la valeur de h est remplacée par 2dc, dc représentant la distance de l’axe neutre à la fibre extrême en compression (voir la figure).
QUESTION: (2014) Je calcule la résistance à la flexion d’une section à symétrie simple en I non maintenue latéralement et ayant des semelles d’épaisseurs différentes. Quelle doit être la valeur de t dans les expressions de βx et de Cw fournies dans l’alinéa 13.6 (e) de S16-09?
RÉPONSE: Dans les deux expressions, la valeur de « d-t » peut être la distance entre les centres de gravité des semelles. Cw peut également être calculée à l’aide de la formule fournie sous Built-up Sections dans la Partie 6 du Handbook of Steel Construction de l’ICCA.
QUESTION: (AUTOMNE2012) Comment dois-je calculer la résistance élastique à la flexion d’une plaque en porte-à-faux soumise à un déversement?nal buckling?
RÉPONSE: Pour une plaque encastrée soumise à un moment de flexion selon son axe fort mais sans soutien latéral, le Guide to Stability Design Criteria for Metal Structures, 6th Edition (R.D. Ziemian, John Wiley & Sons, 2010) fournit des expressions pour le moment de flambement élastique (Mu), en fonction de la hauteur de du point d’application de la charge. Par exemple, lorsque la plaque est soumise à une charge ponctuelle à son extrémité:
a) Pour une charge sur la surface supérieure:
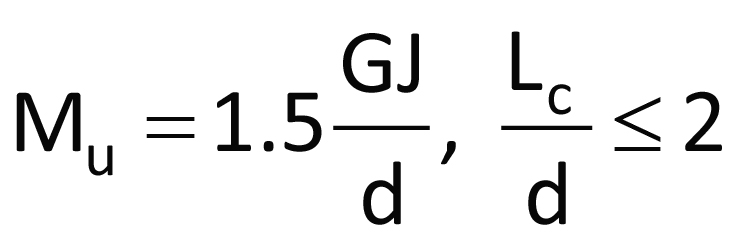
où E et G sont les modules d’élasticité et de cisaillement, respectivement, Iy est l’axe principal d’inertie minimale, « J » la constante de torsion de St-Venant, « d » la profondeur de la plaque et Lc, la longueur du porte-à-faux.
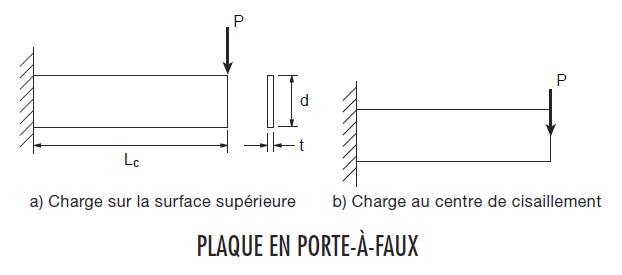 NOTE: Dans le numéro 44 de la revue Avantage Acier, cette rubrique fait référence au moment de déversement élastique de porte-à-faux indiqué dans le Guide to Stability Design Criteria for Metal Structures, 6e édition. Comparativement à des études récentes utilisant l’analyse par éléments finis, l’expression « Mc = 1.5GJ/d » offre des valeurs imprudentes pour les plaques (section rectangulaire) et les longs porte-à-faux de profilé en I qui sont sujets au déversement. Il faut éviter de l’utiliser pour les porte-à-faux en plaques qui sont plus longs que le double de leur profondeur.
NOTE: Dans le numéro 44 de la revue Avantage Acier, cette rubrique fait référence au moment de déversement élastique de porte-à-faux indiqué dans le Guide to Stability Design Criteria for Metal Structures, 6e édition. Comparativement à des études récentes utilisant l’analyse par éléments finis, l’expression « Mc = 1.5GJ/d » offre des valeurs imprudentes pour les plaques (section rectangulaire) et les longs porte-à-faux de profilé en I qui sont sujets au déversement. Il faut éviter de l’utiliser pour les porte-à-faux en plaques qui sont plus longs que le double de leur profondeur.
QUESTION: (ÉTÉ2012) Lors de la conception de poutres continues et de poutres du système Gerber (Figure 1), peut-on déduire les points d’inflexion contreventés latéralement contre le déversement?
RÉPONSE: Il ne faut pas confondre les points d’inflexion dans le diagramme des moments fléchissants verticaux avec les points d’inflexion dans le flambement latéral. En général, on ne connaît pas le flambement latéral au stade de la conception. Les points d’inflexion dans le diagramme des moments fléchissants ne coïncidant pas avec ceux du flambement latéral, ils ne doivent pas être considérés comme étant contreventés latéralement, sauf s’ils sont contreventés.

