
A quantity that is often used when designing a steel beam according to CSA Standard S16 Clause 13.6 is Lu , the longest unbraced length with which the beam will reach either Mr = φ Mp or Mr = φ My , depending on the class of the cross-section.
In other words, whenever the unsupported length of a beam is less than Lu , the member is considered laterally supported and will reach its full moment capacity. Lu also appears in several design tables in Part 5 of the Handbook of Steel Construction, such as the Beam Selection and Beam Load Tables.
As the S16 Standard does not provide an explicit expression for Lu , engineers sometimes wonder how it is derived. When calculating its value, it is assumed that the beam is simply supported and subject to a uniform bending moment, as shown in Figure 1.

Figure 1
Deriving the formula for Lu for doubly-symmetric wide-flange beams involves a bit of algebra. A Class 1 or 2 beam (maximum factored moment resistance, Mr = φ Mp = φ Zx Fy) will be assumed in the following calculations.
The factored moment resistance of a laterally unsupported beam is given by S16:19 Clause 13.6(a):
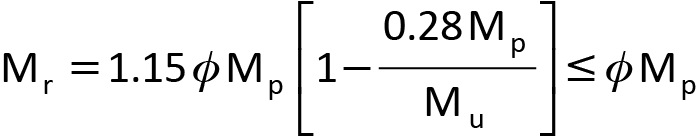
Eq. 1
when Mu > 0.67 Mp . Mu is the elastic lateral-torsional buckling moment of a laterally unbraced beam of length, L, given by:
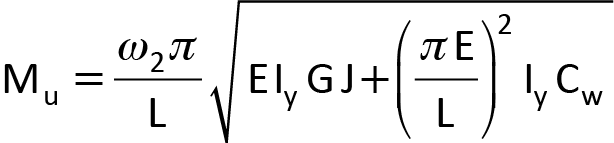
Eq. 2
and ω2 = 1.0 for a beam under uniform moment.
Setting Mr = φ Mp in Equation 1, and substituting the expression for Mu from Equation 2:
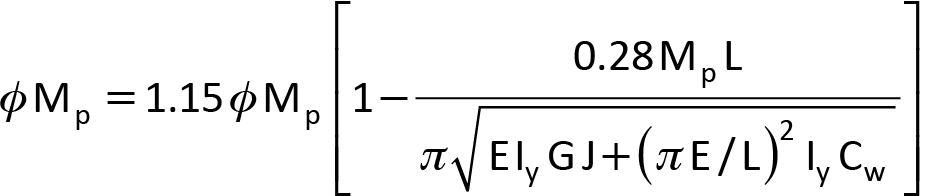
Eq. 3
Re-arranging Equation 3 so that the square root appears on the left-hand side:
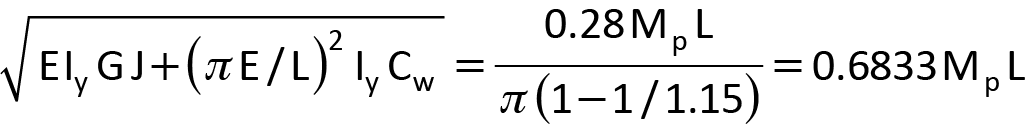
Eq. 4
After squaring both sides and multiplying throughout by L2, we get the following:
![]()
Eq. 5
If we define X = L2, Equation 5 is a quadratic expression of the form:
![]()
Eq. 6
whose solution is:
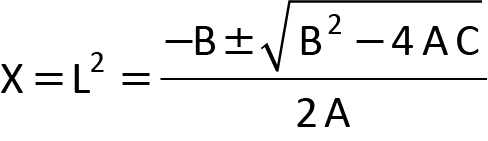
Eq. 7
If we identify A, B and C in Equation 6 with the corresponding terms in Equation 5, and retain the plus sign in front of the square root, Equation 7 yields the following solution for Lu:
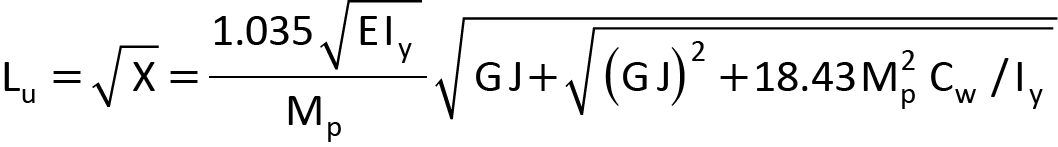
Eq. 8








